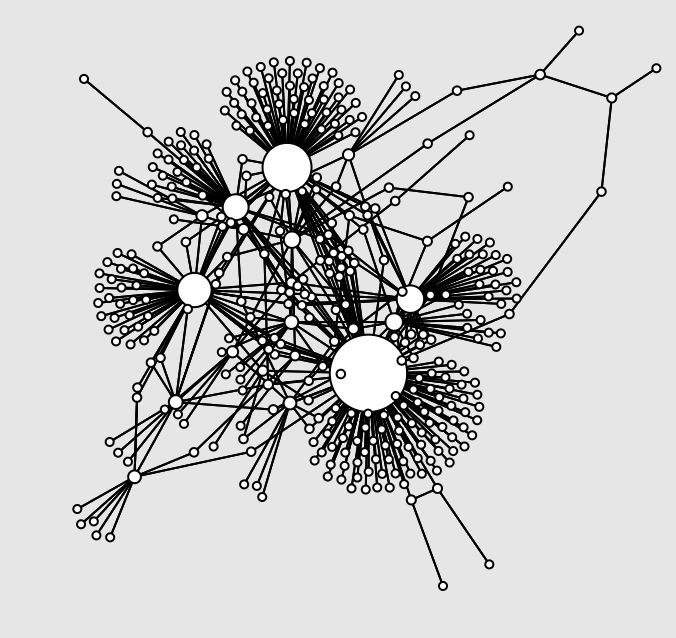
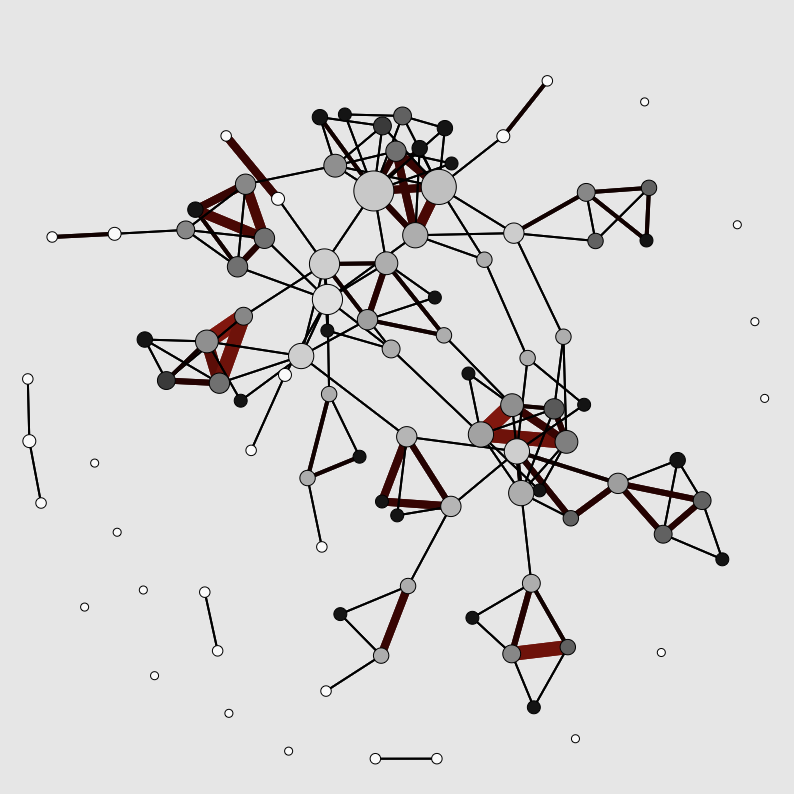
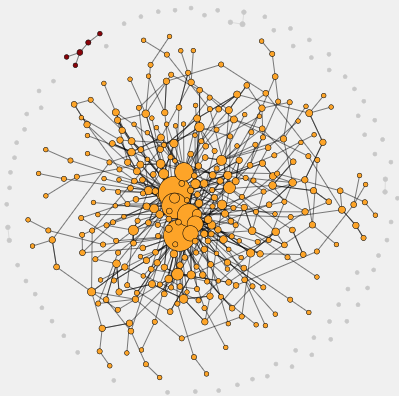
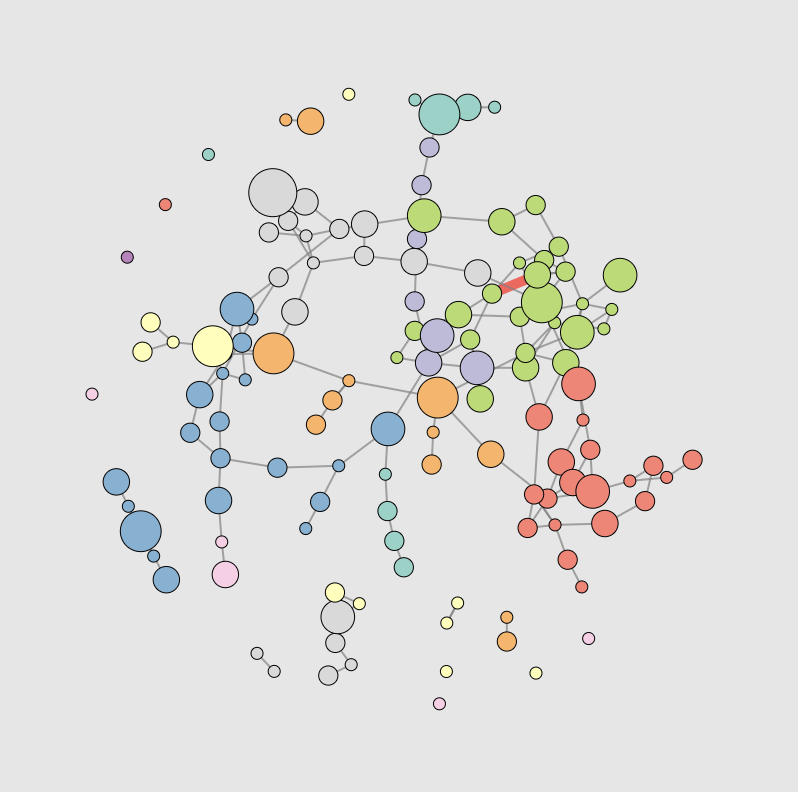
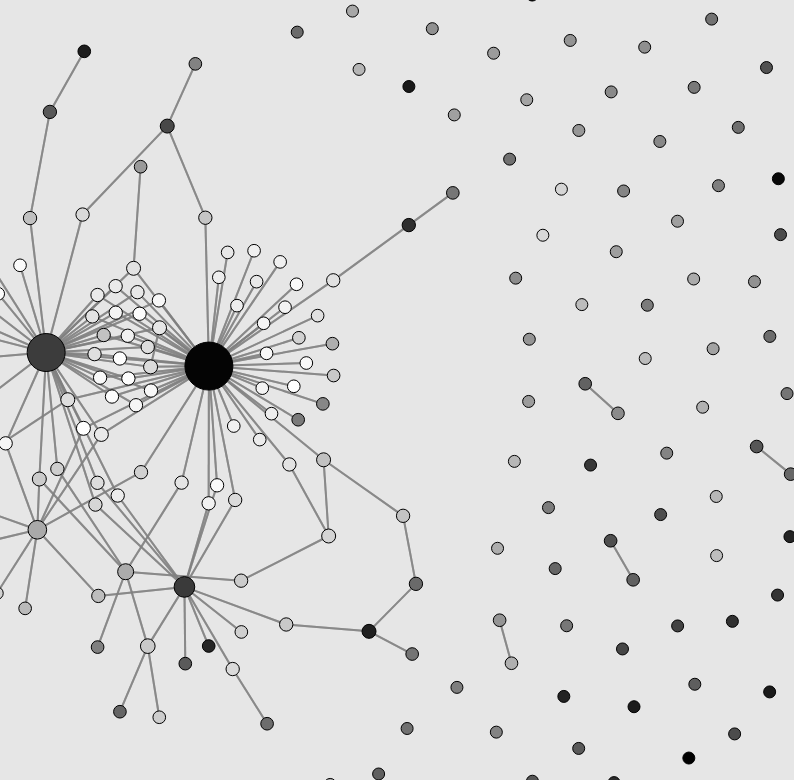
“Clustershuck”
A network growth model that naturally yields clusters and heterogeneity
This explorable illustrates how strong heterogeneities, cluster-like structures and high variability in node connectivities can naturally emerge in growing networks. The mechanism explored here is very simple: When a new node is added to the network it picks another target node at random. Instead of linking to it, the new node establishes a link to one of the target’s neighbors.
“Jujujajáki networks”
The emergence of communities in weighted networks
This explorable illustrates a dynamic network model that was designed to capture the emergence of community structures, heterogeneities and clusters that are frequently observed in social networks. Clusters are characterized by a high probability that a person’s ‘friends are also friends’. In this model not only the connectivity evolves but also the strength of links between nodes. The model was orginally proposed by Jussi Kumpula, Jukka-Pekka Onnela, Jari Saramäki, János Kertész and Kimmo Kaski.
“The Blob”
A network's giant component
This explorable illustrates an important feature of complex networks: the emergence of the giant component. Networks often have multiple components. A component is a part of the network where we can find a path between any two nodes by traversing links.
“Echo Chambers”
A model for opinion dynamics
This explorable illustrates a network model that captures how opinion dynamics might work in a population and how clusters of uniform opinion might naturally emerge from an initially random system. The model is a variant of a model introduced by P. Holme and M. Newman in a 2006 paper: Nonequilibrium phase transition in the coevolution of networks and opinions.
“Knitworks”
Growing complex networks
This explorable illustrates network growth based on preferential attachment, a variant of the Barabasi-Albert model that was introduced to capture strong heterogeneities observed in many natural and technological networks. It has become a popular model for scale-free networks in nature.
Preferential attachment means that nodes that enter the network during a growth process preferentially connect to nodes with specific properties. In the original system, they preferentially connect to existing nodes that are already well connected, increasing their connectivity even further. This rich get richer effect generates networks in which a few nodes are very strongly connected and very many nodes poorly.