“Horde of the Flies”
The Vicsek-Model
This explorable illustrates one of the most famous and most fundamental models for the emergence of flocking, swarming and synchronized behavior in animal groups. The model was originally published in a 1995 paper by Tamás Vicsek and co-workers and is therefore called the Vicsek-Model. The model can explain why transitions to flocking behavior in groups of animals are often not gradual. Instead, one can expect a sudden emergence of flocking and synchronized movements if a critical density is crossed.
“Spin Wheels”
Phase-coupled oscillators on a lattice
This explorable illustrates pattern formation, interesting and beautiful properties of oscillators that are spatially arranged on a lattice and interact with their neighbors. Oscillators and their interaction are described by the famous Kuramoto Model for phase coupled oscillators. The model is amazing, because on one hand it is conceptually quite simple, on the other it holds a number of unexpected dynamical secrets that you can discover here.
“Swårmalätørs”
Oscillators that sync and swarm
This explorable illustrates how remarkable spatio-temporal patterns can emerge when two dynamical phenomena, synchronization and collective motion, are combined. In the model, a bunch of oscillators move around in space and interact. Each oscillator has an internal oscillatory phase. An oscillator’s movement and change of internal phase both depend on the positions and internal phases of all other oscillators. Because of this entanglement of spatial forces and phase coupling the oscillators are called swarmalators.
“Come Together”
Chemotaxis in Dictyostelium discoideum
This explorable illustrates how simple, single-cell organisms can manage to aggregate into multi-cellular structures by emitting and responding to chemical signals. Individual cells respond by orienting towards a chemical signal and moving up its gradient, a process known as chemotaxis. The combination of synchronized signal emission and chemotaxis yields collective behavior with beautiful spatial branching patterns during the aggregation process.
“Janus Bunch”
Dynamics of two-phase coupled oscillators
“I sing well-tempered”
The Ising Model
This explorable illustrates one of the most famous models in statistical mechanics: The Ising Model. The model is structurally very simple and captures the properties and dynamics of magnetic materials, such as ferromagnets. It is so general that it is also used to describe opinion dynamics in populations and collective behavior in animal groups.
“Anomalous Itinerary”
Lévy flights
This explorable illustrates the properties of a class of random walks known as Lévy flights. To get the most out of this explorable, you may want to check out the explorable Albert & Carl Friedrich on ordinary random walks and diffusion first.
“Hopfed Turingles”
Pattern Formation in a simple reaction-diffusion system
With this explorable you can discover a variety of spatio-temporal patterns that can be generated with a very famous and simple autocatalytic reaction diffusion system known as the Gray-Scott model. In the model two substances $U$ and $V$ interact and diffuse in a two-dimensional container. Although only two types of simple reactions occur, the system generates a wealth of different stable and dynamic spatio-temporal patterns depending on system parameters.
“Albert & Carl Friedrich”
Random Walks & Diffusion
This explorable illustrates the geometric and dynamic properties of the physical process of diffusion and its intimate relation to a mathematical object known as a random walk. It also illustrates graphically the implications of the central limit theorem that explains why we so often (normally) observe Gaussian distributions in nature. In the context of random walks this means that in the long run and from a great distance the paths of different types of walks become statistically indistiguishable.
“Critically Inflammatory”
A forrest fire model
This explorable illustrates, as a representative of a broad range of dynamic phenomena, a simple model for the spatial spread of forest fires and the dynamic patterns they generate. In the model two antagonistic processes interplay, the reproductive growth of vegetation that continuously covers the landscape with trees susceptible to fires and spontaneously seeded (lightning strikes) forest fires that spread across areas of dense vegetation.
“Dr. Fibryll & Mr. Glyde”
Pulse-coupled oscillators
This explorable illustrates pattern formation in excitable media. The example explored here in a system of pulse-coupled oscillators that are arranged on a two-dimensional lattice and interact with their neighbors by delivering excitatory pulses to them and receiving them in return. This model is sometimes used to study synchronization and can capture the dynamics of activation in layers of neurons as well as the spatial patterns of signaling molecules that play a role in microbial aggregation processes.
“Stranger Things”
Strange attractors
This explorable illustrates the structure and beauty of strange attractors of two-dimensional discrete maps. These maps generate sequences of pairs of number $(x_n,y_n)$ where the index $n=0,1,2,…$ denotes the step of the iteration process that starts at the point $(x_0,y_0)$. The map is defined by two functions $f(x,y)$ and $g(x,y)$ that determine the point $(x_{n+1},y_{n+1})$ given $(x_{n},y_{n})$:
“Kelp!!!”
A stochastic cellular automaton
This explorable illustrates how fractal growth patterns can be generated by stochastic cellular automata. Cellular automata are spatially and temporally discrete dynamical systems that are conceptually very straightforward but can generate unexpected complex behavior, often fractal-like structures reminiscent of patterns we see in natural systems.
“Knitworks”
Growing complex networks
This explorable illustrates network growth based on preferential attachment, a variant of the Barabasi-Albert model that was introduced to capture strong heterogeneities observed in many natural and technological networks. It has become a popular model for scale-free networks in nature.
Preferential attachment means that nodes that enter the network during a growth process preferentially connect to nodes with specific properties. In the original system, they preferentially connect to existing nodes that are already well connected, increasing their connectivity even further. This rich get richer effect generates networks in which a few nodes are very strongly connected and very many nodes poorly.
“If you ask your XY”
The XY model of statistical mechanics
This explorable illustrates pattern formation and dynamics in the $XY$-model, an important model in statistical mechanics for studying phase-transitions and other phenomena. It’s a generalization of the famous Ising-Model. The $XY$-model is actually quite simple.
“Ride my Kuramotocycle!”
The Kuramoto model
This explorable illustrates the Kuramoto model for phase coupled oscillators. This model is used to describe synchronization phenomena in natural systems, e.g. the flash synchronization of fire flies or wall-mounted clocks.
“Barista's Secret”
Percolation on a lattice
This explorable illustrates a process known as percolation. Percolation is a topic very important for understanding processes in physics, biology, geology, hydrology, horstology, epidemiology, and other fields. Percolation theory is the mathematical tool designed for understanding these processes.
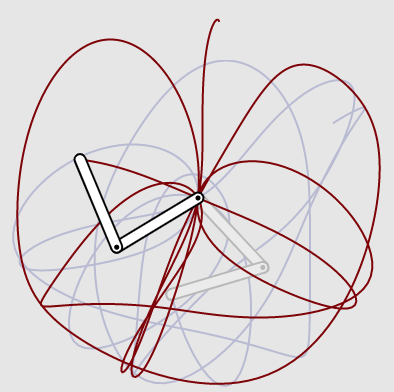
“Double Trouble”
The double pendulum
This explorable illustrates the beautiful dynamical features of the double pendulum, a famous idealized nonlinear mechanical system that exhibits deterministic chaos. The double pendulum is essentially two simple pendula joined by a bearing. It’s a classic complex system in which a simple setup generates rich and seemingly unpredictable behavior. The only force that is acting on it is gravity. There’s no friction.
“Particularly Stuck”
Diffusion Limited Aggregation
This explorable illustrates a process known as diffusion-limited aggregation (DLA). It’s a kinetic process driven by randomly diffusing particles that gives rise to fractal structures, reminiscent of things we see in natural systems. The process has been investigated in a number of scientific studies, e.g. the seminal paper by Witten & Sander.
“Cycledelic”
The spatial rock-paper-scissors game
This explorable of a pattern forming system is derived from a model that was designed to understand co-existance of cyclicly interacting species in a spatially extended model ecosystem. Despite its simplicity, it can generate a rich set of complex spatio-temporal patterns depending on the choice of parameters and initial conditions.
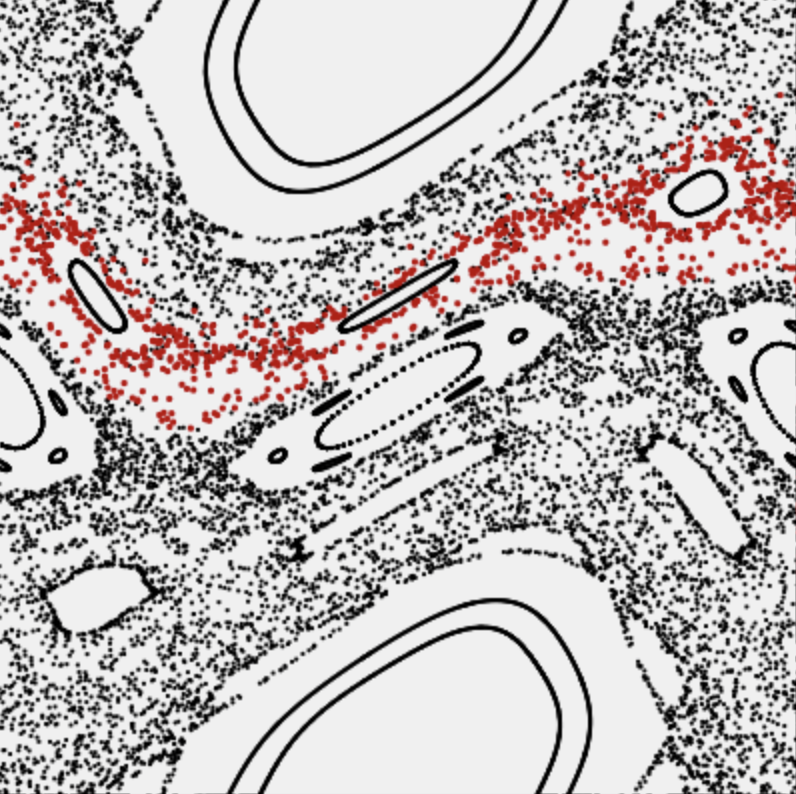
“Kick it like Chirikov”
The kicked rotator (standard map)
In this explorable you can investigate the dynamics of a famous two-dimensional, time discrete map, known as the standard or Chirikov–Taylor map, one of the most famous dynamical systems that exhibits deterministic chaos. It is almost identical to the “Kicked Rotator”, an idealized physical system in which a rotating rod is periodically kicked by an external force.
“Keith Haring's Mexican Hat”
Pattern Formation by Local Excitation and Long-Range Inhibition
This explorable illustrates one of the most basic mechanisms for spontaneous pattern formation: Local excitation and long range inhibition. This mechanism or similar ones are responsible for patterns observed in many natural systems, such as neural tissue, animal fur and spatial heterogeneity in social systems.