“Spin Wheels”
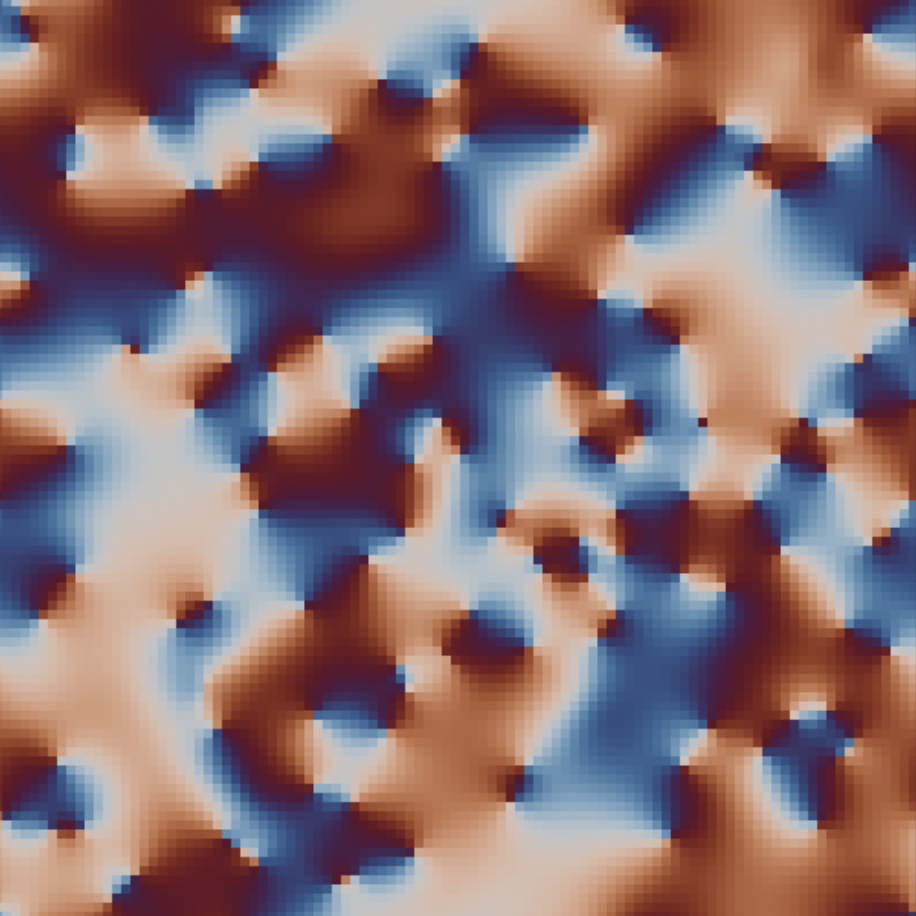
Phase-coupled oscillators on a lattice
This explorable illustrates pattern formation, interesting and beautiful properties of oscillators that are spatially arranged on a lattice and interact with their neighbors. Oscillators and their interaction are described by the famous Kuramoto Model for phase coupled oscillators. The model is amazing, because on one hand it is conceptually quite simple, on the other it holds a number of unexpected dynamical secrets that you can discover here.
“Swårmalätørs”
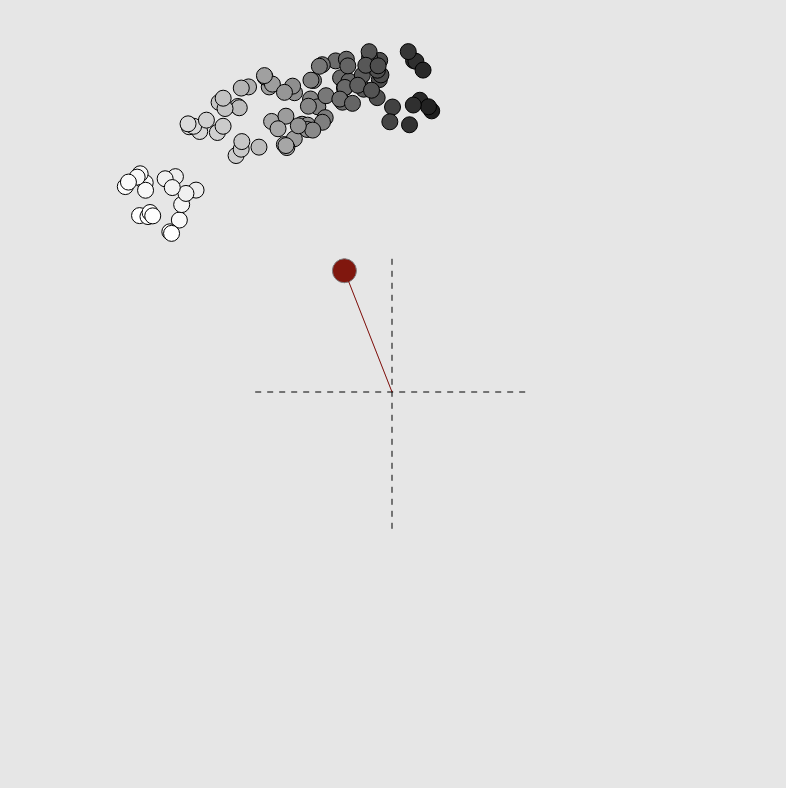
Oscillators that sync and swarm
This explorable illustrates how remarkable spatio-temporal patterns can emerge when two dynamical phenomena, synchronization and collective motion, are combined. In the model, a bunch of oscillators move around in space and interact. Each oscillator has an internal oscillatory phase. An oscillator’s movement and change of internal phase both depend on the positions and internal phases of all other oscillators. Because of this entanglement of spatial forces and phase coupling the oscillators are called swarmalators.
“Janus Bunch”
Dynamics of two-phase coupled oscillators
“Dr. Fibryll & Mr. Glyde”
Pulse-coupled oscillators
This explorable illustrates pattern formation in excitable media. The example explored here in a system of pulse-coupled oscillators that are arranged on a two-dimensional lattice and interact with their neighbors by delivering excitatory pulses to them and receiving them in return. This model is sometimes used to study synchronization and can capture the dynamics of activation in layers of neurons as well as the spatial patterns of signaling molecules that play a role in microbial aggregation processes.
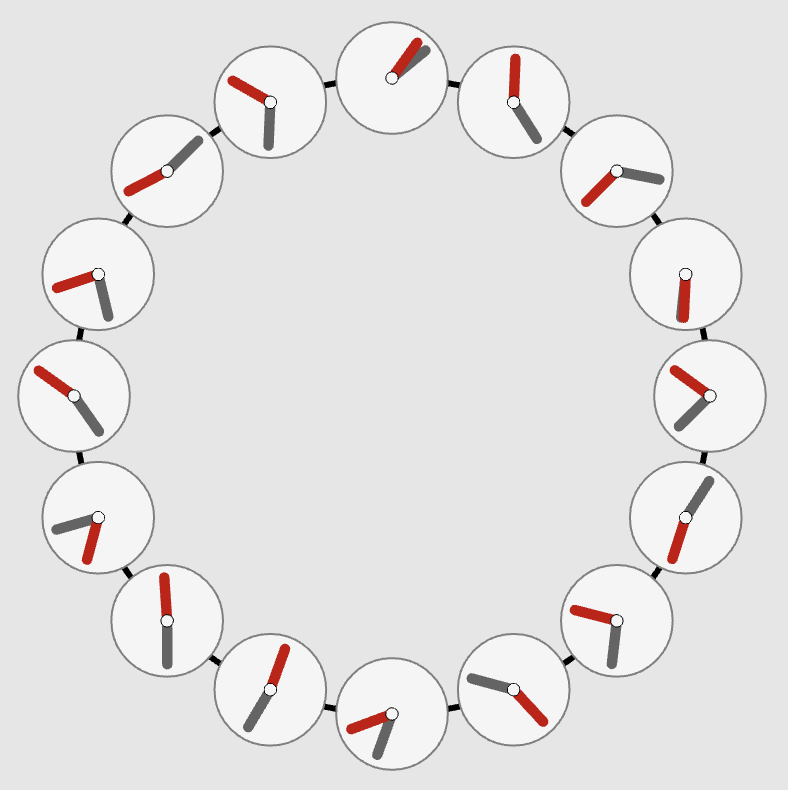
“Ride my Kuramotocycle!”
The Kuramoto model
This explorable illustrates the Kuramoto model for phase coupled oscillators. This model is used to describe synchronization phenomena in natural systems, e.g. the flash synchronization of fire flies or wall-mounted clocks.