“Prime Time”
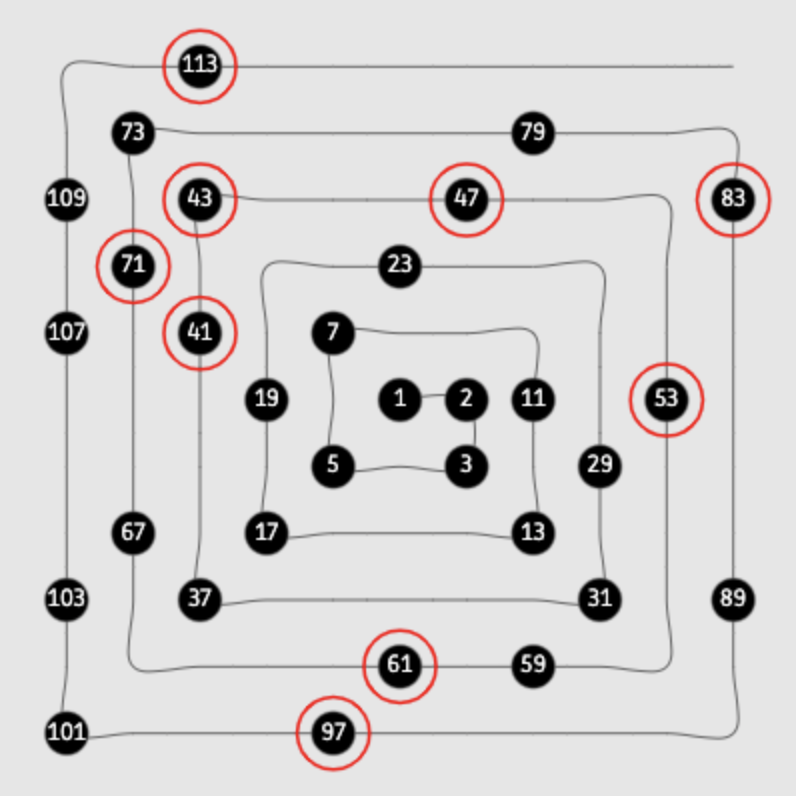
The distribution of primes along number spirals
This explorable is about prime numbers. It illustrates interesting patterns that emerge if you arrange the positive natural numbers $1,2,3,….$ and so forth in a regular pattern in the plane and look at the distribution of the primes in the arrangement. Although prime numbers, as one might expect, don’t follow some regular repetitive pattern, they are also not distributed completely at random. Instead, in all arrangements streaks and fragments of neighboring primes emerge. These structures are related to prime generating polynomials like the famous polynomial discovered by Leonard Euler.
“Stranger Things”
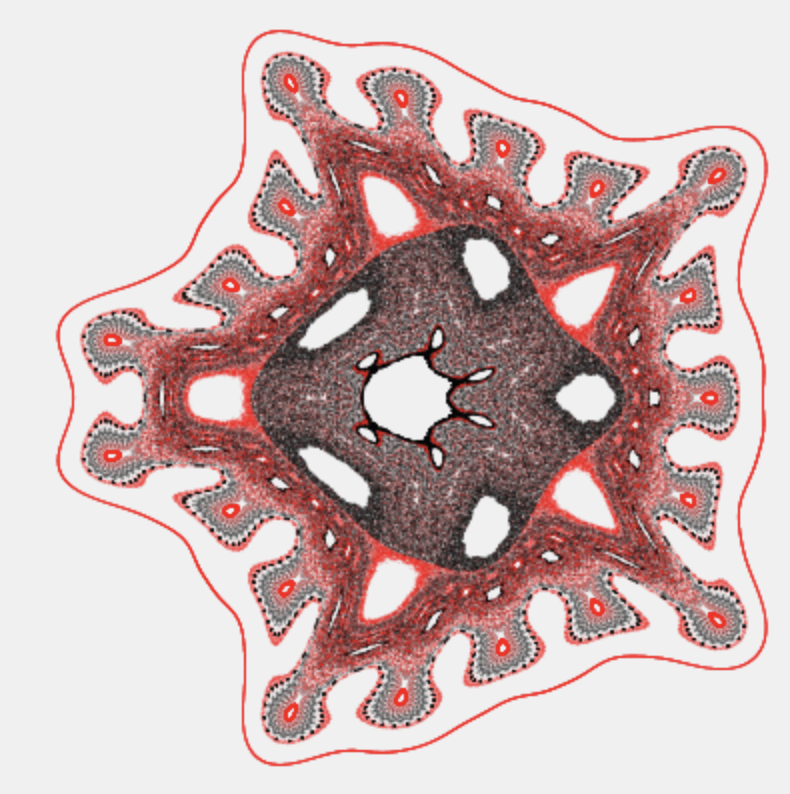
Strange attractors
This explorable illustrates the structure and beauty of strange attractors of two-dimensional discrete maps. These maps generate sequences of pairs of number $(x_n,y_n)$ where the index $n=0,1,2,…$ denotes the step of the iteration process that starts at the point $(x_0,y_0)$. The map is defined by two functions $f(x,y)$ and $g(x,y)$ that determine the point $(x_{n+1},y_{n+1})$ given $(x_{n},y_{n})$:
“Kelp!!!”
A stochastic cellular automaton
This explorable illustrates how fractal growth patterns can be generated by stochastic cellular automata. Cellular automata are spatially and temporally discrete dynamical systems that are conceptually very straightforward but can generate unexpected complex behavior, often fractal-like structures reminiscent of patterns we see in natural systems.
“Hokus Fractus!”
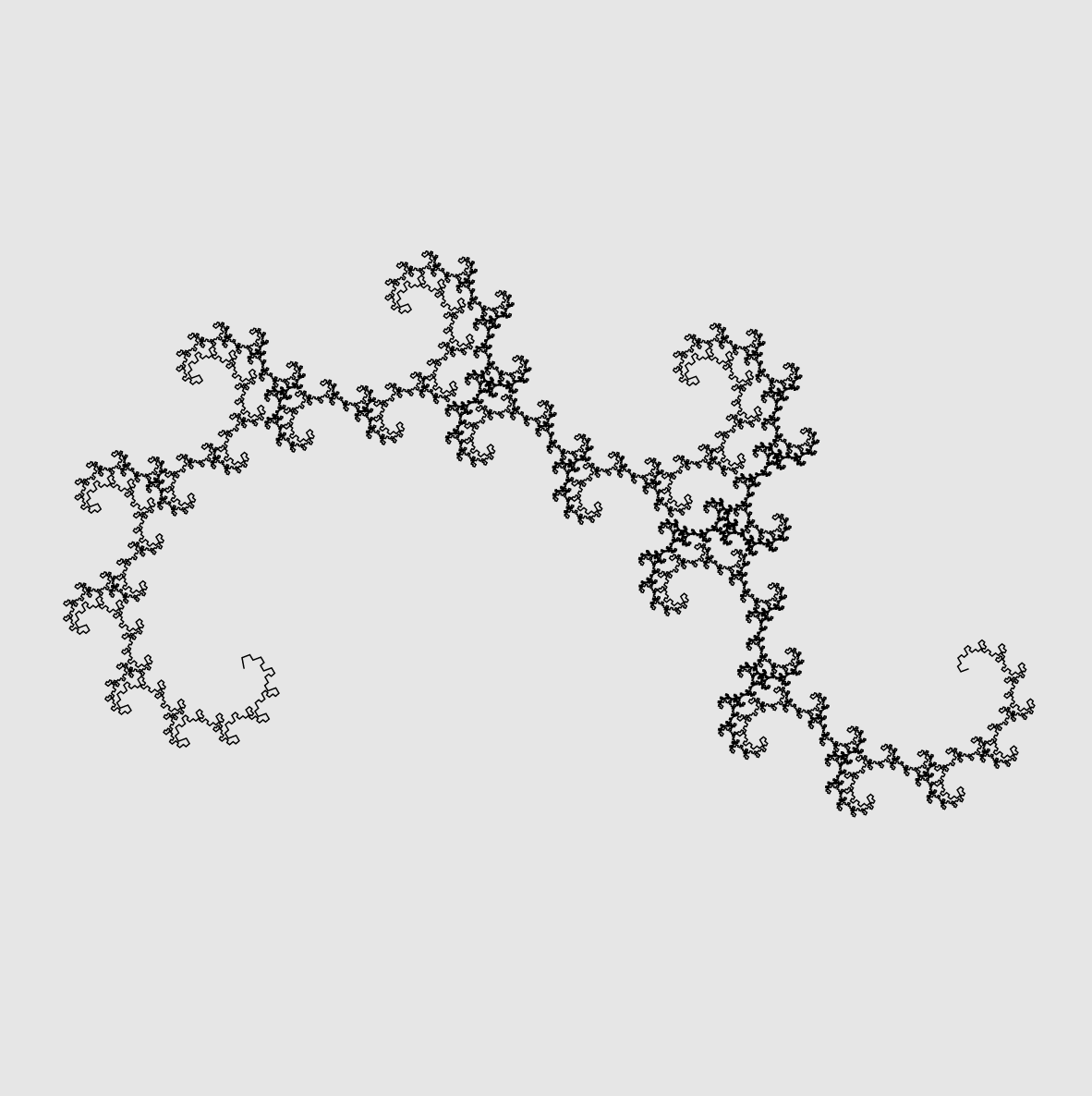
Famous fractals
This explorable illustrates one of the simplest ways to generate fractals by an iteration process in which elements of a structure are replaced by a smaller version of the whole structure. Similar to the Weeds & Trees Explorable, these structures can be viewed as Lindenmayer systems. A great variety of examples of such fractals exist.
“Particularly Stuck”
Diffusion Limited Aggregation
This explorable illustrates a process known as diffusion-limited aggregation (DLA). It’s a kinetic process driven by randomly diffusing particles that gives rise to fractal structures, reminiscent of things we see in natural systems. The process has been investigated in a number of scientific studies, e.g. the seminal paper by Witten & Sander.
“Kick it like Chirikov”
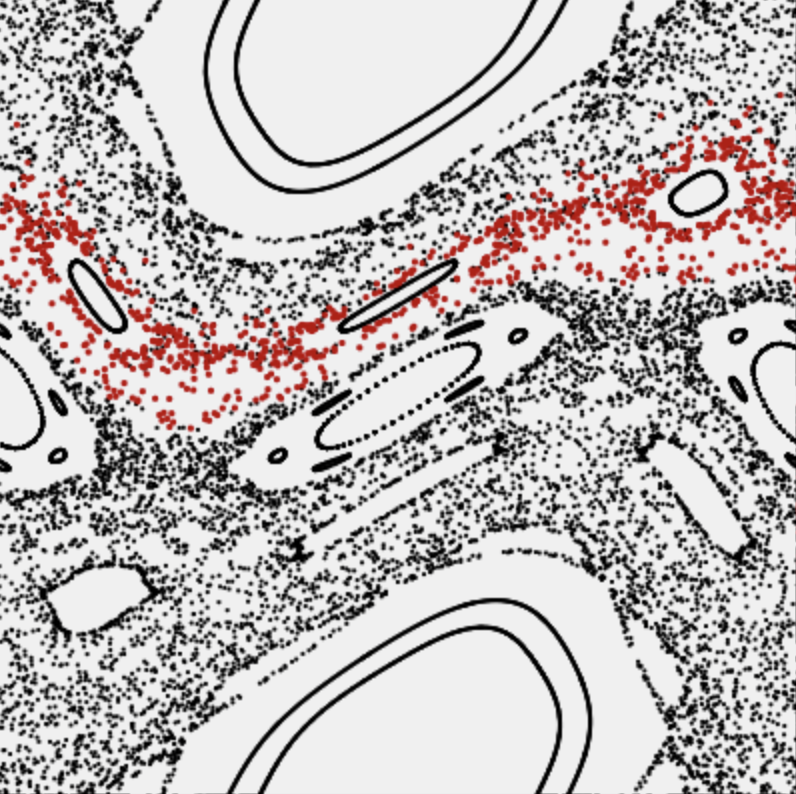
The kicked rotator (standard map)
In this explorable you can investigate the dynamics of a famous two-dimensional, time discrete map, known as the standard or Chirikov–Taylor map, one of the most famous dynamical systems that exhibits deterministic chaos. It is almost identical to the “Kicked Rotator”, an idealized physical system in which a rotating rod is periodically kicked by an external force.
“Weeds & Trees”
Lindenmayer Systems
This explorable illustrates how fractal patterns observed in natural systems, particularly structural properties of some plants, can approximately be modeled by simple iterative models. Sometimes these models are refered to as Lindenmayer systems.