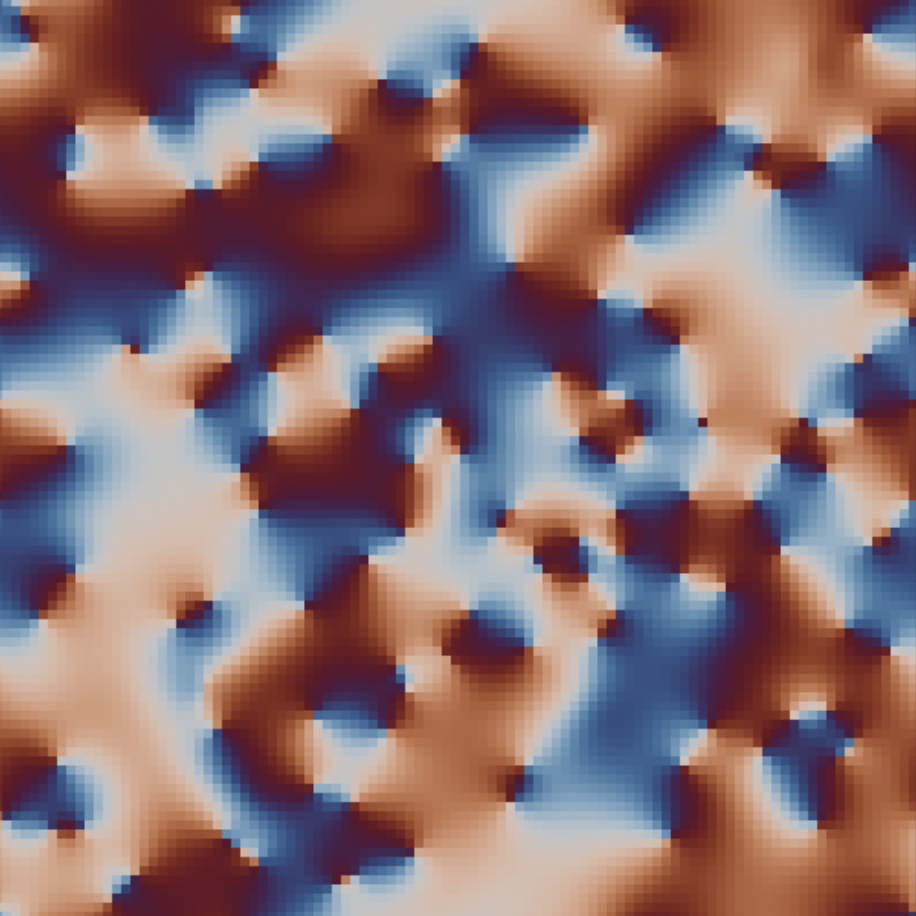
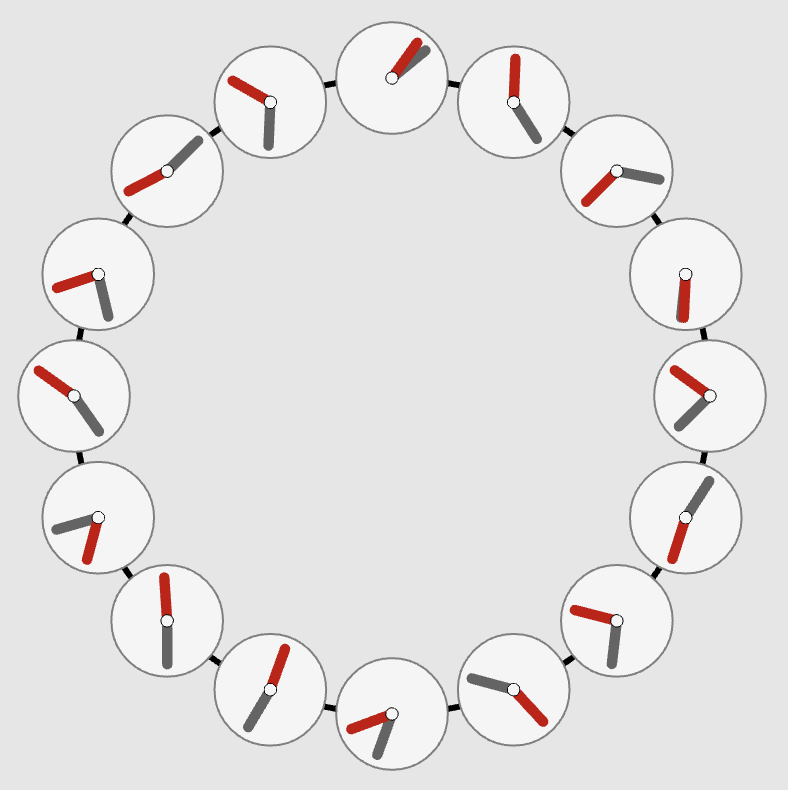
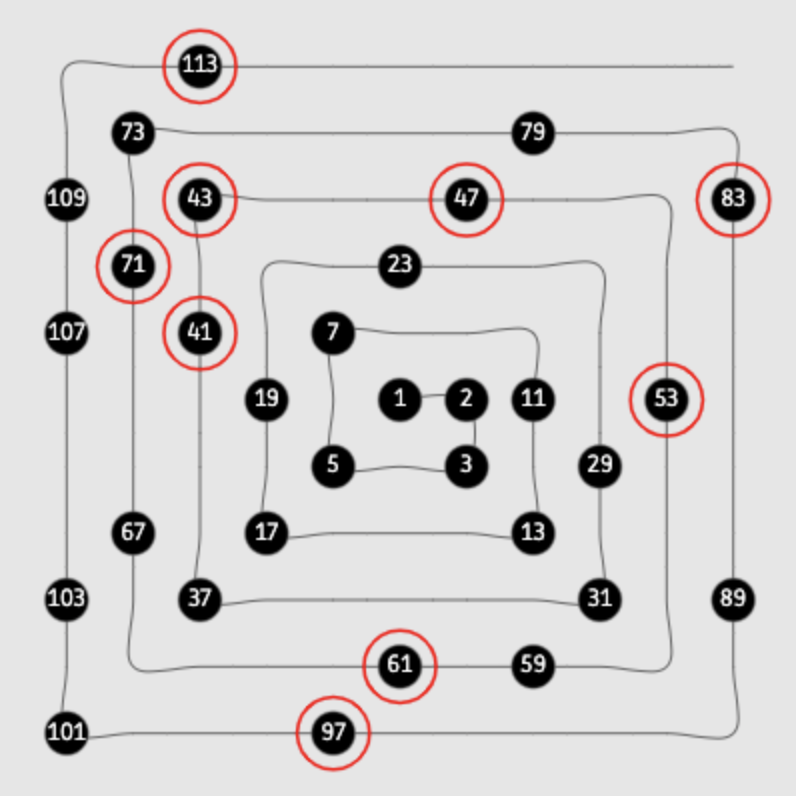
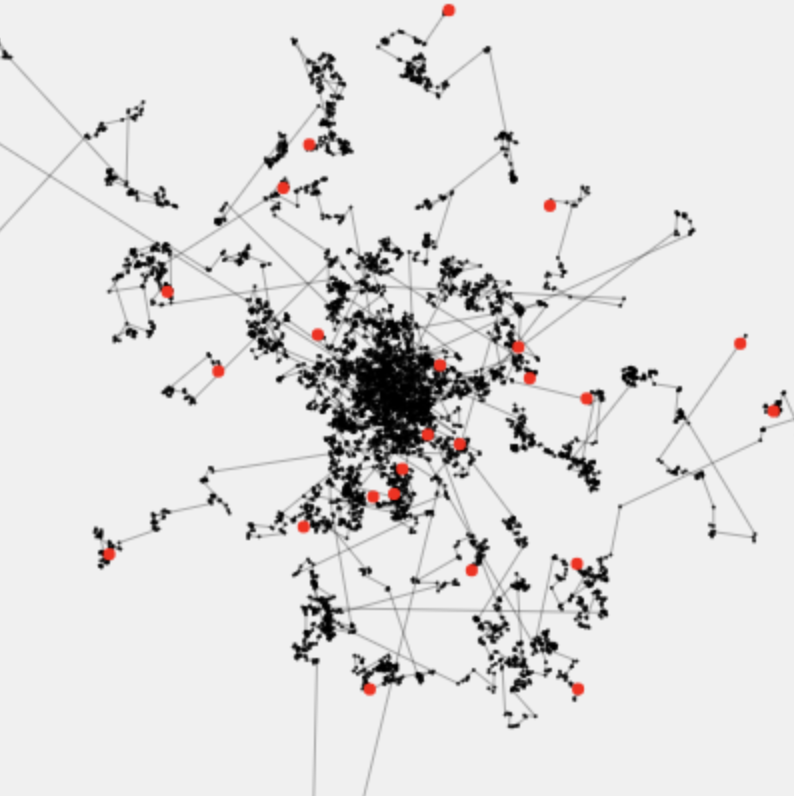
“Spin Wheels”
Phase-coupled oscillators on a lattice
This explorable illustrates pattern formation, interesting and beautiful properties of oscillators that are spatially arranged on a lattice and interact with their neighbors. Oscillators and their interaction are described by the famous Kuramoto Model for phase coupled oscillators. The model is amazing, because on one hand it is conceptually quite simple, on the other it holds a number of unexpected dynamical secrets that you can discover here.
“Swårmalätørs”
Oscillators that sync and swarm
This explorable illustrates how remarkable spatio-temporal patterns can emerge when two dynamical phenomena, synchronization and collective motion, are combined. In the model, a bunch of oscillators move around in space and interact. Each oscillator has an internal oscillatory phase. An oscillator’s movement and change of internal phase both depend on the positions and internal phases of all other oscillators. Because of this entanglement of spatial forces and phase coupling the oscillators are called swarmalators.
“Janus Bunch”
Dynamics of two-phase coupled oscillators
“Nah dah dah nah nah... (Opus, 1984)”
Conway's Game of Life
“Prime Time”
The distribution of primes along number spirals
This explorable is about prime numbers. It illustrates interesting patterns that emerge if you arrange the positive natural numbers $1,2,3,….$ and so forth in a regular pattern in the plane and look at the distribution of the primes in the arrangement. Although prime numbers, as one might expect, don’t follow some regular repetitive pattern, they are also not distributed completely at random. Instead, in all arrangements streaks and fragments of neighboring primes emerge. These structures are related to prime generating polynomials like the famous polynomial discovered by Leonard Euler.
“Anomalous Itinerary”
Lévy flights
This explorable illustrates the properties of a class of random walks known as Lévy flights. To get the most out of this explorable, you may want to check out the explorable Albert & Carl Friedrich on ordinary random walks and diffusion first.
“Hopfed Turingles”
Pattern Formation in a simple reaction-diffusion system
With this explorable you can discover a variety of spatio-temporal patterns that can be generated with a very famous and simple autocatalytic reaction diffusion system known as the Gray-Scott model. In the model two substances $U$ and $V$ interact and diffuse in a two-dimensional container. Although only two types of simple reactions occur, the system generates a wealth of different stable and dynamic spatio-temporal patterns depending on system parameters.
“Albert & Carl Friedrich”
Random Walks & Diffusion
This explorable illustrates the geometric and dynamic properties of the physical process of diffusion and its intimate relation to a mathematical object known as a random walk. It also illustrates graphically the implications of the central limit theorem that explains why we so often (normally) observe Gaussian distributions in nature. In the context of random walks this means that in the long run and from a great distance the paths of different types of walks become statistically indistiguishable.
“Dr. Fibryll & Mr. Glyde”
Pulse-coupled oscillators
This explorable illustrates pattern formation in excitable media. The example explored here in a system of pulse-coupled oscillators that are arranged on a two-dimensional lattice and interact with their neighbors by delivering excitatory pulses to them and receiving them in return. This model is sometimes used to study synchronization and can capture the dynamics of activation in layers of neurons as well as the spatial patterns of signaling molecules that play a role in microbial aggregation processes.
“Stranger Things”
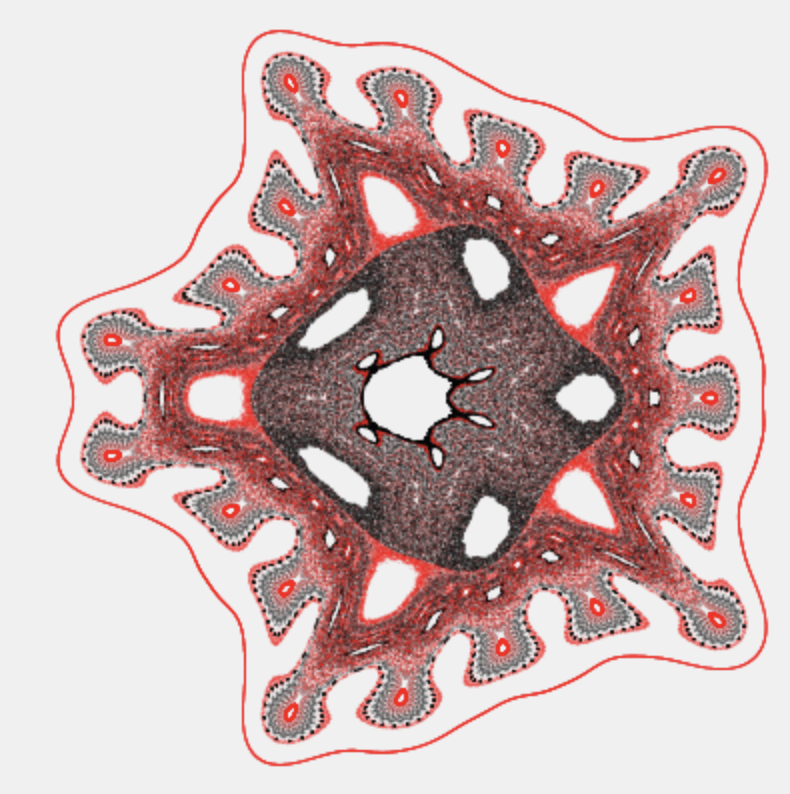
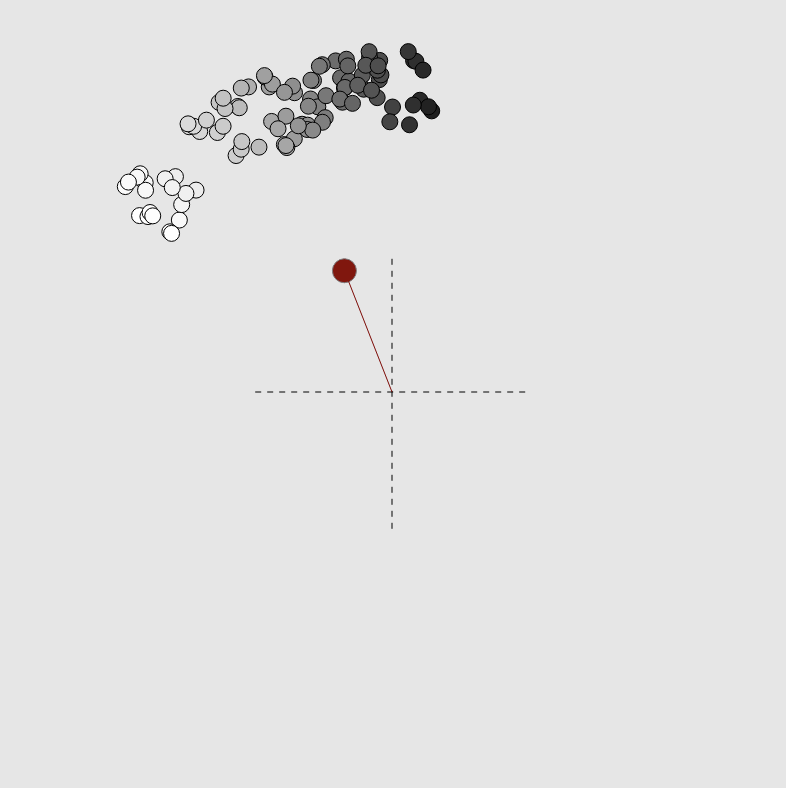
Strange attractors
This explorable illustrates the structure and beauty of strange attractors of two-dimensional discrete maps. These maps generate sequences of pairs of number $(x_n,y_n)$ where the index $n=0,1,2,…$ denotes the step of the iteration process that starts at the point $(x_0,y_0)$. The map is defined by two functions $f(x,y)$ and $g(x,y)$ that determine the point $(x_{n+1},y_{n+1})$ given $(x_{n},y_{n})$:
“Kelp!!!”
A stochastic cellular automaton
This explorable illustrates how fractal growth patterns can be generated by stochastic cellular automata. Cellular automata are spatially and temporally discrete dynamical systems that are conceptually very straightforward but can generate unexpected complex behavior, often fractal-like structures reminiscent of patterns we see in natural systems.
“Ride my Kuramotocycle!”
The Kuramoto model
This explorable illustrates the Kuramoto model for phase coupled oscillators. This model is used to describe synchronization phenomena in natural systems, e.g. the flash synchronization of fire flies or wall-mounted clocks.
“Hokus Fractus!”
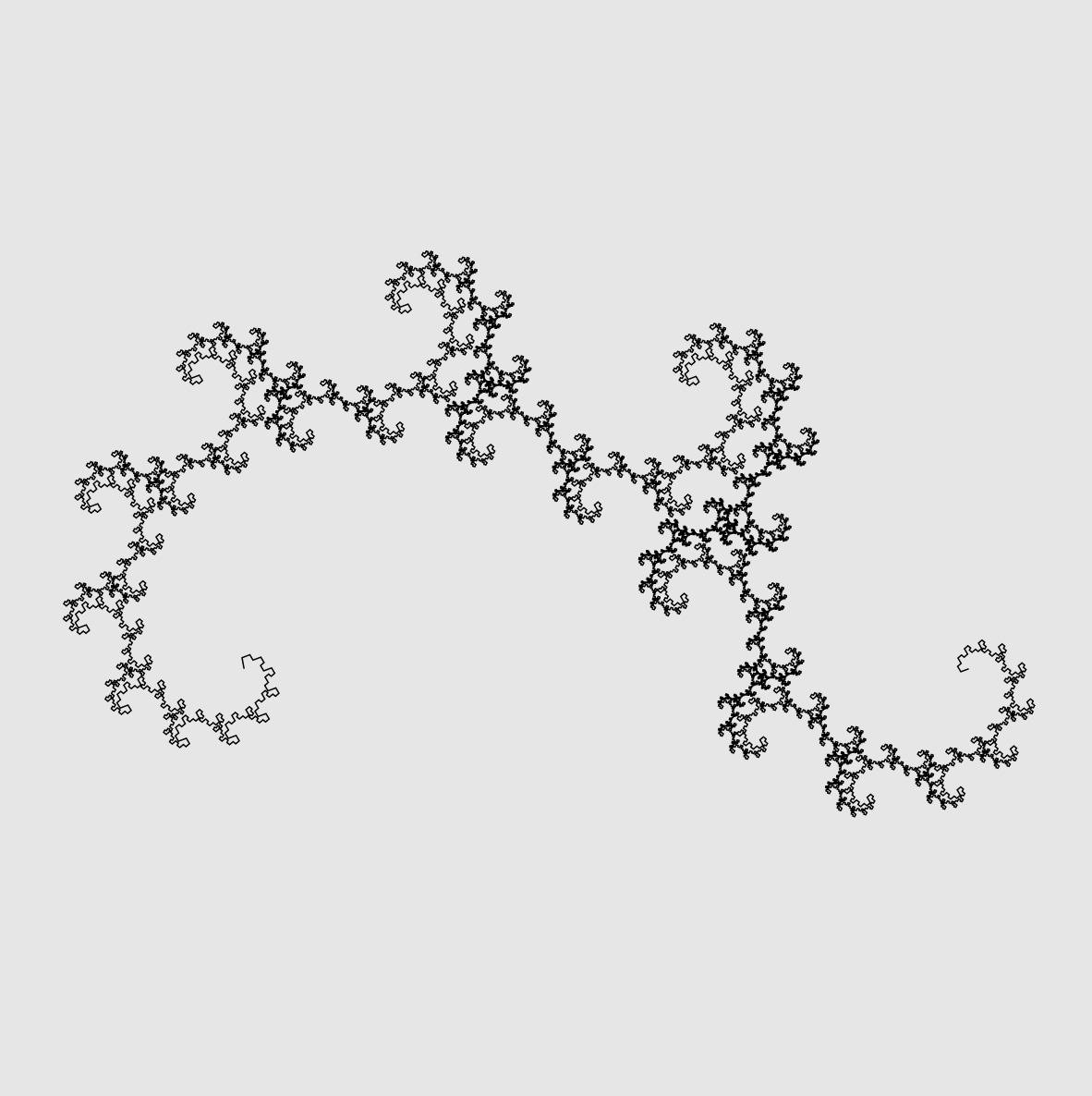
Famous fractals
This explorable illustrates one of the simplest ways to generate fractals by an iteration process in which elements of a structure are replaced by a smaller version of the whole structure. Similar to the Weeds & Trees Explorable, these structures can be viewed as Lindenmayer systems. A great variety of examples of such fractals exist.
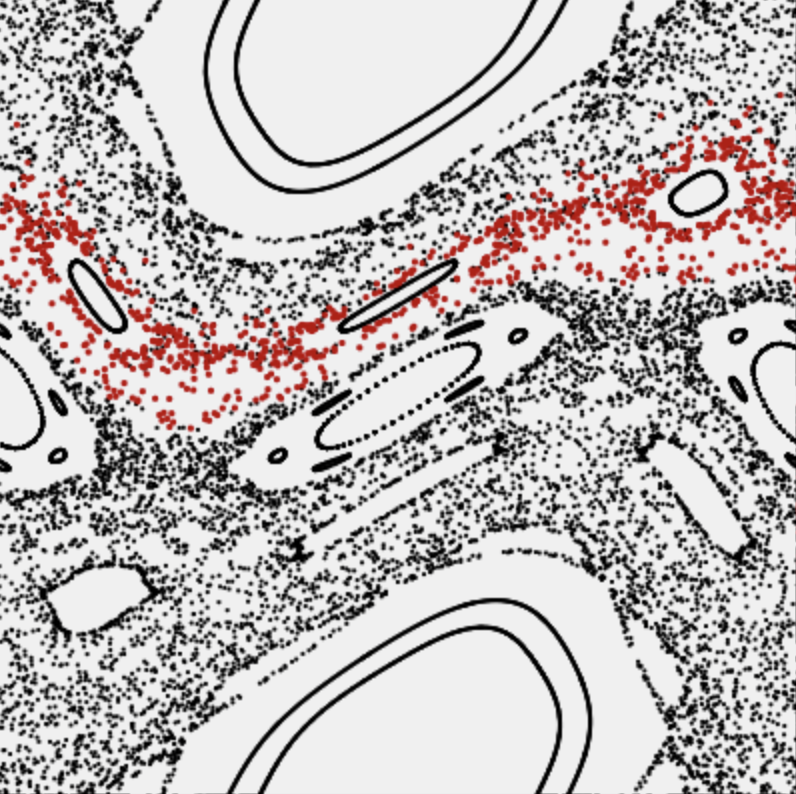
“Kick it like Chirikov”
The kicked rotator (standard map)
In this explorable you can investigate the dynamics of a famous two-dimensional, time discrete map, known as the standard or Chirikov–Taylor map, one of the most famous dynamical systems that exhibits deterministic chaos. It is almost identical to the “Kicked Rotator”, an idealized physical system in which a rotating rod is periodically kicked by an external force.
“Weeds & Trees”
Lindenmayer Systems
This explorable illustrates how fractal patterns observed in natural systems, particularly structural properties of some plants, can approximately be modeled by simple iterative models. Sometimes these models are refered to as Lindenmayer systems.