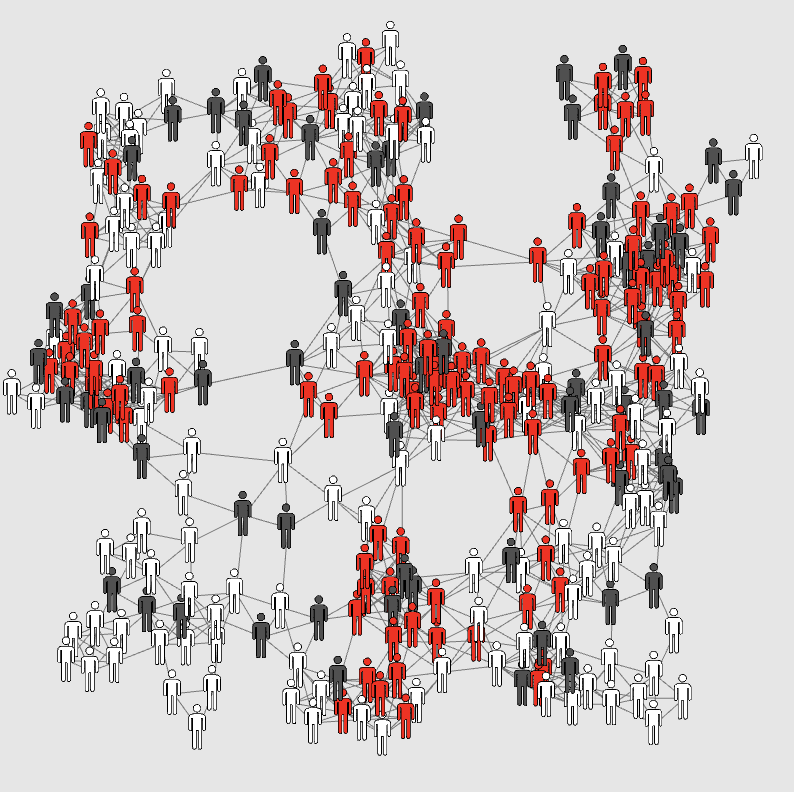
This explorable illustrates one of the most famous and most fundamental models for the emergence of flocking, swarming and synchronized behavior in animal groups. The model was originally published in a 1995 paper by Tamás Vicsek and co-workers and is therefore called the Vicsek-Model. The model can explain why transitions to flocking behavior in groups of animals are often not gradual. Instead, one can expect a sudden emergence of flocking and synchronized movements if a critical density is crossed.

This explorable illustrates how remarkable spatio-temporal patterns can emerge when two dynamical phenomena, synchronization and collective motion, are combined. In the model, a bunch of oscillators move around in space and interact. Each oscillator has an internal oscillatory phase. An oscillator’s movement and change of internal phase both depend on the positions and internal phases of all other oscillators. Because of this entanglement of spatial forces and phase coupling the oscillators are called swarmalators.

This explorable illustrates the dynamics of the Schelling model named after economist and Nobel laureate Thomas Schelling (1921-2016). Although this model has been applied in different contexts, it is best known for its ability to capture geographical ethnic segregation of human populations and cities based on very simple principles.

This explorable illustrates the wealth of dynamical states exhibited in a network of Janus Oscillators. Janus oscillators are a generalization of ordinary phase coupled oscillators (see Complexity Explorable “Ride my Kuramotocycle!”). Like the Roman god Janus, a Janus oscillator has two “faces”, each corresponding to a distinct internal phase variable. This slight generalization produces a surprisingly large array of complex phenomena in a simple ring arrangement. Press play and keep on reading…

This explorable features an agent based model for road traffic and congestion. The model captures a phenomenon that most of us have witnessed on highways: phantom traffic jams, also known as traffic shocks or ghost jams. These are spontaneously emergent congested segments that move slowly and oppositely to the traffic. The explorable illustrates that phantom jams are more likely to occur if the variability in car speeds is higher:

This explorable illustrates one of the most famous models in statistical mechanics: The Ising Model. The model is structurally very simple and captures the properties and dynamics of magnetic materials, such as ferromagnets. It is so general that it is also used to describe opinion dynamics in populations and collective behavior in animal groups.

This explorable illustrates, as a representative of a broad range of dynamic phenomena, a simple model for the spatial spread of forest fires and the dynamic patterns they generate. In the model two antagonistic processes interplay, the reproductive growth of vegetation that continuously covers the landscape with trees susceptible to fires and spontaneously seeded (lightning strikes) forest fires that spread across areas of dense vegetation.

This explorable illustrates pattern formation in excitable media. The example explored here in a system of pulse-coupled oscillators that are arranged on a two-dimensional lattice and interact with their neighbors by delivering excitatory pulses to them and receiving them in return. This model is sometimes used to study synchronization and can capture the dynamics of activation in layers of neurons as well as the spatial patterns of signaling molecules that play a role in microbial aggregation processes.

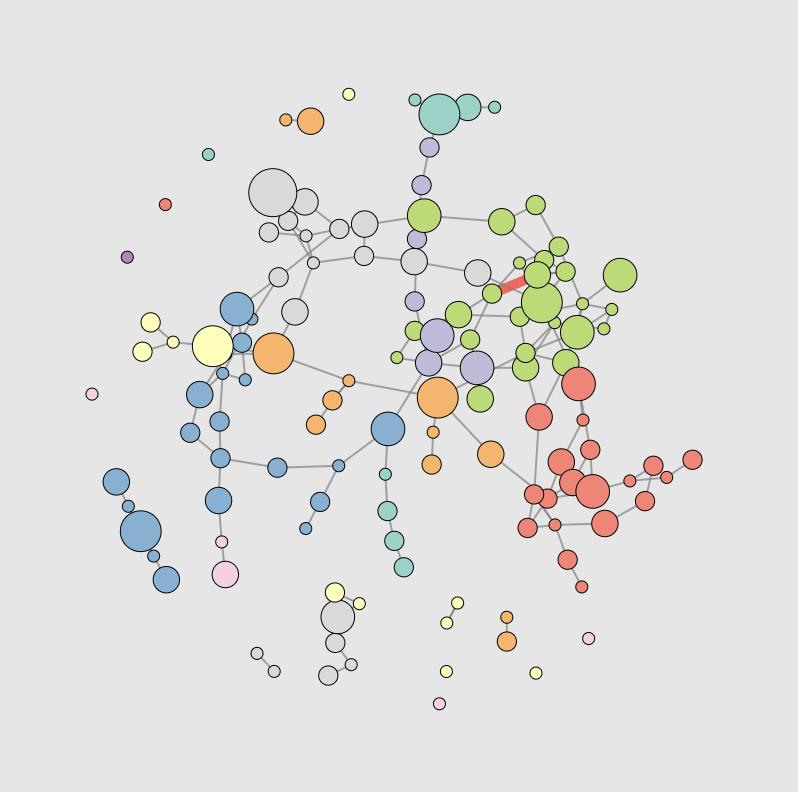
This explorable illustrates an important feature of complex networks: the emergence of the giant component. Networks often have multiple components. A component is a part of the network where we can find a path between any two nodes by traversing links.

This explorable illustrates the mechanism of herd immunity. When an infectious disease spreads in a population, an individual can be protected by a vaccine that delivers immunity. But there’s a greater good. Immunization not only projects the individual directly. The immunized person will also never transmit the disease to others, effectively reducing the likelihood that the disease can proliferate in the population. Because of this, a disease can be eradicated even if not the entire population is immunized. This population wide effect is known as herd immunity.

This explorable illustrates a network model that captures how opinion dynamics might work in a population and how clusters of uniform opinion might naturally emerge from an initially random system. The model is a variant of a model introduced by P. Holme and M. Newman in a 2006 paper: Nonequilibrium phase transition in the coevolution of networks and opinions.

This explorable illustrates pattern formation and dynamics in the $XY$-model, an important model in statistical mechanics for studying phase-transitions and other phenomena. It’s a generalization of the famous Ising-Model. The $XY$-model is actually quite simple.

This explorable illustrates the Kuramoto model for phase coupled oscillators. This model is used to describe synchronization phenomena in natural systems, e.g. the flash synchronization of fire flies or wall-mounted clocks.

This explorable illustrates a process known as percolation. Percolation is a topic very important for understanding processes in physics, biology, geology, hydrology, horstology, epidemiology, and other fields. Percolation theory is the mathematical tool designed for understanding these processes.

This explorable illustrates the behavior of a contagion process near its critical point. Contagion processes, for example transmissible infectious diseases, typically exhibit a critical point, a threshold below which the disease will die out, and above which the disease is sustained in a population. Interesting dynamical things happen when the system is near its critical point.

This explorable illustrates one of the most basic mechanisms for spontaneous pattern formation: Local excitation and long range inhibition. This mechanism or similar ones are responsible for patterns observed in many natural systems, such as neural tissue, animal fur and spatial heterogeneity in social systems.