EXPLORABLES

13 October, 2022

This explorable illustrates how a remarkably simple mathematical model for pedestrian dynamics can capture a number of features that are observed in actual pedestrian flows on walkways for example. In the model individual pedestrians move with an individual anticipated speed and direction. When obstacles get in their way, either physical obstacles or other pedestrians, walkers experience a repulsive social force, that alters their velocity and current direction to avoid collision. This alone is sufficient to produce a variety of patterns that are reminiscent of actual pedestrian dynamics. The explorable is a simplified variant of a series of beautiful models introduced by Dirk Helbing that have found a wide range of application, e.g. panic dynamics, crowd turbulence, traffic jams and more.

Press Play and keep on reading….

Presentation Slide

This is how it works

Initially, we have $N=25$ walkers on a circular walkway that either prefer to walk around it in a clockwise (white) or counter-clockwise (dark grey) direction. The walkers have approximately the same natural walking speed with a bit of variation between them.

When a walker encounters a wall or another person, the walker experiences a repulsive force that increases with decreasing distance to the obstacle. The direction of the repulsive force acts along the line that connects the walker with the obstacle. As a consequence the walkers natural walking direction and speed is altered by this social force.

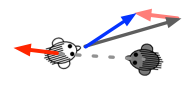
For example in the above illustration, the white walker prefers a velocity (grey arrow) but experiences a social force by the dark fellow that is approaching (red arrow). This perturbs the anticipated velocity to become the blue arrow.

Observe this

Initially, not much is going on in the arena, the concentration of walkers is low, every now and then pairs of individuals avoid collisions and move around one another. When the system equilibrates, you may see traces of lanes forming in which individuals of the same polarity (bright or dark) move in a row.

Lane formation

Now increase the number of people, e.g. to $N=100$ by selecting the number in the control panel. Quickly, you will see that the social force generates lanes of individuals that move in one direction. Increase the number of individuals to $N=200$, you will see 2-4 lanes in the arena.

Speed variation

By default, all walkers prefer approximately the same speed. With the speed variability slider, you can increase the variability of individuals’ speeds. With $N=200$ walkers, increase the variability to its maximum value. (You can also change the mean speed with the corresponding slider). Let the system equilibrate again. You should be able to observe areas of congestion, high densities of individuals that have difficultly to pass one another. The variablity in speed impedes the overall flow and also breaks the lane formation. This effect is similar to phantom traffic jams that you can explore in the “Berlin 8 a.m."-Explorable.

Difficulties for minorities

With the directional bias slider, you can change the proportion of individuals that move in one of the other direction. For a total of $N=200$ individuals, try to establish a system in which only a tiny fraction, say $10$ move into one direction, and the great majority in the other. You should see that the minorty fails to establish lanes and has difficulty to move agains the bulk current.

Obstacles

In the control panel, you see three switches for different physical obstacles that you can place into the arena. Before you do, choose a small population of walkers, say $N=50$ and sequentially turn on the obstacles. You should be able to observe that the flow of individuals moves smoothly around the obstacles, also changing the shape of lanes.

When you increase the density of walkers and increase the speed variability the situation at the obstacles can become quite erratic as walkers try to squeeze through the gaps.

Again, set up the proportion of both populations in a strongly biased way. You should see that individuals of the minority group sometimes can never pass an obstacle, because the majority flow doesn’t permit it.

Miscellaneous

There also the option of using different symbols to represent the walkers. Instead of little heads you can use bare circles, this sometimes helps to see the flow better. Also, you can choose “Manlios”. This options was implemented to express my deep gratitude to Manlio De Domenico, who was very sad that until now no Complexity Explorable has been dedicated to him. With this Explorable I hope I have somewhat relieved Manlio’s grief.